[논문리뷰] - Grad-CAM : Visual Explanations from Deep Networks via Gradient-based Localization, ICCV 2017

인공지능은 이미 거의 모든 분야에서 다양한 용도로 사용되고 있습니다. 대부분 성능이 뛰어나지만 때로는 오작동을 합니다. 하지만 현재 대부분 AI는 딥러닝 기반 모델이므로 오작동하는 이유에 대해서 파악하기 힘들다는 단점을 갖고 있습니다.

CAM 예시

이러한 문제를 해결하고자 이미지 분야에서는 Class Activation Mapping(CAM) 이라는 방법이 고안되었습니다. CAM은 이미지 분류 모델로 사진을 분류할 때 사진의 어느 부분이 영향력을 끼치는지를 추출할 수 있는 방법론입니다. 다만 이 방법론을 사용하기 위해서는 논문에서 제시한 것처럼 모델의 구조 변경이 필요하기 때문에 이미 학습한 모델은 구조를 변경한 후 재학습이 필요합니다. 또한 구조를 변경함으로써 성능이 미미하게 하락한다는 단점이 존재합니다.

다행히 CAM방법론이 제시된 다음해에 모델의 구조를 변경하지 않으면서 CAM을 사용할 수 있는 방법론이 ICCV(2017) 에서 공개되었습니다. 오늘 포스팅은 모델의 구조를 변경하지 않으면서 CAM을 사용할 수 있는 방법론에 대해 다룬 논문인 Grad-CAM을 리뷰하도록 하겠습니다. 이 글은 Grad-CAM:Visual Explanations from Deep Networks via Gradient-based Localization 논문 을 참고하여 정리하였음을 먼저 밝힙니다. 논문 그대로를 리뷰하기보다는 생각을 정리하는 목적으로 제작하고 있기 때문에 실제 내용과 다른점이 존재할 수 있습니다. 혹시 제가 잘못 알고 있는 점이나 보안할 점이 있다면 댓글 부탁드립니다.

Short Summary

이 논문의 큰 특징 3가지는 아래와 같습니다.

모델의 구조를 변경하지 않으면서 객체의 위치를 추출하는 방법인 Grad-CAM 을 제시합니다.
높은 해상도의 이미지에서 분류에 영향을 주는 pixcel을 추출하는 방법인 Guided Grad-CAM 을 제시합니다.
이미지에서 오분류 확률을 높이는 지역을 추출할 수 있는 새로운 해석 방식을 제시합니다.

[1] CAM 적용방법

Grad-CAM에 대해 리뷰하기 전에 기존 CAM의 특징과 적용방법에 대해서 알아 보겠습니다. CAM의 목표는 이미지 분류 문제를 학습한 모델을 이용하여 분류를 할 때 모델은 이미지의 어느 부분을 보는지를 표시한 Class Activation MAP을 추출하는 것입니다. 이는 학습된 모델의 weight($w_k^c$)와 이미지를 모델에 넣어 생성된 feature map($A_{i,j}^k$)을 이용하여 만들 수 있습니다.

CAM 구조 예시

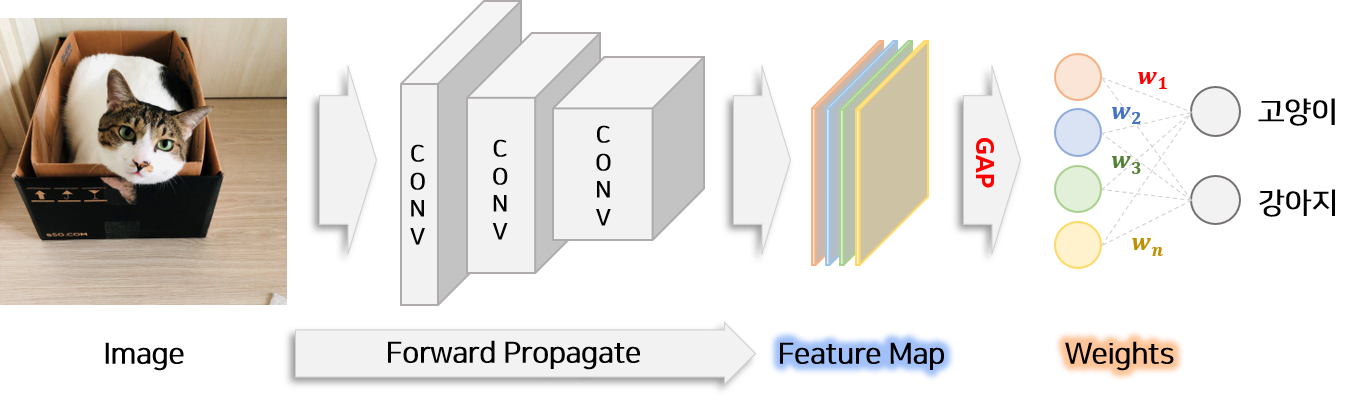
위 그림에서 처럼 이미지를 넣으면 모델의 forward pass에 따라 feature map($A_{i,j}^k$)이 생성됩니다. 이 feature map은 Global Average Pooling(GAP) layer와 연결되어 있고 이후 한번에 FC layer + softmax함수를 거쳐 각 class 확률을 출력합니다. FC layer가 의미하는 것은 각 feature map($A_{i,j}^k$)이 class($c$)에 얼마나 영향을 미치는지를 나타내는 weight($w_k^c$)와 같습니다. 따라서 feature map($A_{i,j}^k$)와 weight($w_k^c$) 을 이용하여 좌표($i, j$)가 특정 class($c$)에 영향을 미치는 정도($M_{i,j}^c$)를 수식으로 나타내면 아래와 같습니다.

$F^k = \frac{1}{Z} \sum_{i,j} A_{i,j}^k$ $Y^c = \sum_k w_k^c F^k$ $Y^c = \sum_k w_k^c \frac{1}{Z} \sum_{i,j} A_{i,j}^k$ $Y^c = \sum_{i,j} \frac{1}{Z} \sum_k w_k^c A_{i,j}^k$ $Y^c = \sum_{i,j} M_{i,j}^c$

$A_{i,j}^k$ : feature map k의 가로($i$), 세로($j$)에 해당하는 값
$F^k$ : feature $k$의 Global Average Pooling 값
$Y^c$ : class $c$에 대한 score
$k$ : feature map의 index
$i, j$ : feature map의 가로, 세로 좌표
$w_k^c$ : feature map $k$가 class $c$에 기여하는 weight
$M_{i,j}^c$ : 좌표 $i$, $j$의 class $c$에 대한 영향력(class activation value)

즉 CAM인 $M_{i,j}^c$는 $w_k^c$와 $A_{i,j}^k$로 이루어져 있음을 알 수 있습니다.

CAM 계산 방법 예시

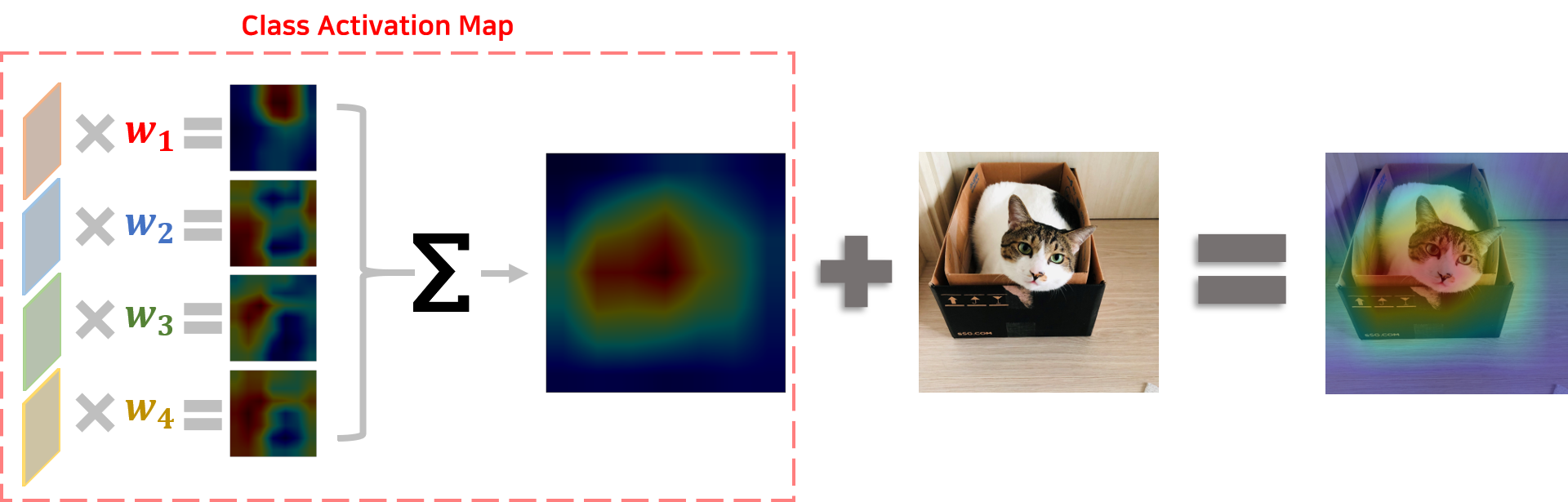
[2] Grad-CAM 적용방법

위 수식처럼 CAM을 구하려면 특정 구조로부터 $w_k^c$가 추출되어야 합니다. 즉 GAP 이후 FC layer 한개만 연결되어 있는 형태여야만 위 수식을 이용하여 CAM을 추출할 수 있습니다. 따라서 CAM 논문에서는 CAM을 사용하기 위해서는 모델을 특정구조로 변경해야 한다고 명시합니다.

Grad-CAM 구조 예시

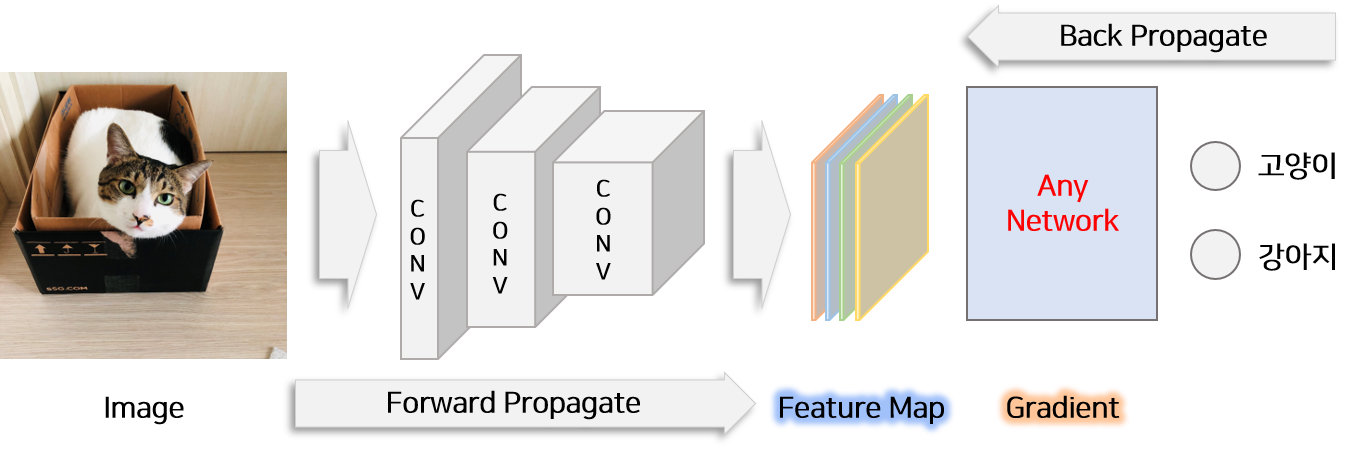
CAM과는 달리 Grad-CAM은 CNN을 사용한 일반적인 모든 구조에서 CAM을 활용할 수 있는 방법을 제시합니다. 바로 weights에 해당하는 부분을 gradient로 대채함으로써 모든 구조에서 특정 class에 feature map 미치는 영향력를 구할 수 있습니다. Grad-CAM에서는 weights에 해당하는 gradient를 다음과 같이 정의합니다.

$w_k^c = \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k}$

$Y^c$는 특정 class c의 score이고 이를 feature map의 각 부분($A_{i,j}^k$)에 대하여 미분한 다음 pixcel($i, j$)에 대하여 모두 더하면 feature map $k$가 class $c$에 미치는 영향인 $w_k^c$를 추출할 수 있습니다. 따라서 CAM에서 정의한 $M_{i,j}^c$를 다시 풀어쓰면 아래와 같습니다.

$M_{i,j}^c = \frac{1}{Z} \sum_k w_k^c A_{i,j}^k$ $M_{i,j}^c = \frac{1}{Z} \sum_k A_{i,j}^k \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k}$ $M_{i,j}^c = \sum_k a_k^c A_{i,j}^k $ $a_k^c = \frac{1}{Z} \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k} $

$a_k^c$ : $w_k^c$를 대채한 gradients

논문에서는 이미지에서 특정 클래스에 긍정적인 영향을 미치는 부분에만 관심이 있으므로 ReLU 비선형 함수를 적용하여 Grad-CAM을 구성한다고 합니다. 따라서 최종적으로 추출된 Grad-CAM의 식은 아래와 같습니다.

$L_{Grad_CAM}^c = ReLU(M_{i,j}^c) = ReLU(\sum_k a_k^c A_{i,j}^k)$

Grad-CAM 도출 과정

Grad-CAM은 CAM의 일반화한 방법입니다. 이를 증명하는 과정은 다음과 같습니다. 분류모델의 output인 class score($Y^c$)를 feature의 average pooling 값인 $F^k$로 미분하여 gradint를 나타내면 아래와 같은 $A_{i,j}^k$에 대한 식으로 표현됩니다.

$\frac{\partial Y^c}{\partial F^k} = \frac{\partial Y^c / \partial A_{i,j}^k}{\partial F^k / \partial A_{i,j}^k}$

$\frac{\partial F^k}{\partial A_{i,j}^k} = \frac{1}{Z}$ 이고, $\frac{\partial Y^c}{\partial F^k} = w_k^c$ 이므로 아래와 같은 식으로 변형이 가능합니다.

$\frac{\partial Y^c}{\partial F^k} = \frac{\partial Y^c}{\partial A_{i,j}^k} \cdot Z$ $w_k^c = \frac{\partial Y^c}{\partial A_{i,j}^k} \cdot Z$

$Z$와 $w_k^c$는 pixcel($i, j$)와는 무관하므로 위의 식을 풀어서 쓰면 $w_k^c$와 gradient 사이의 관계로 변형이 가능합니다.

$\sum_{i,j} w_k^c = \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k} \cdot Z $ $\sum_{i,j} w_k^c = Z \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k} $

($Z=\sum_{i,j}1$)을 이용하여 정리하면 $w_c^k$와 gradient의 관계식을 추출할 수 있습니다.

$Z w_k^c = Z \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k} $ $w_k^c = \sum_{i,j} \frac{\partial Y^c}{\partial A_{i,j}^k} $

CAM에서 제안한 Global Average Pooling(GAP)가 적용된 구조에서 Grad-CAM을 구하는 것과 CAM을 구하는 것은 동일하다는 것을 알 수 있습니다. 즉 CAM은 특정 구조에서 Grad-CAM을 구하는 방법으로 해석할 수 있으므로 Grad-CAM은 CAM의 일반화 방법이라고 논문에서 주장합니다.

[3] Guided Grad-CAM 적용방법

Guided Grad-CAM 예시

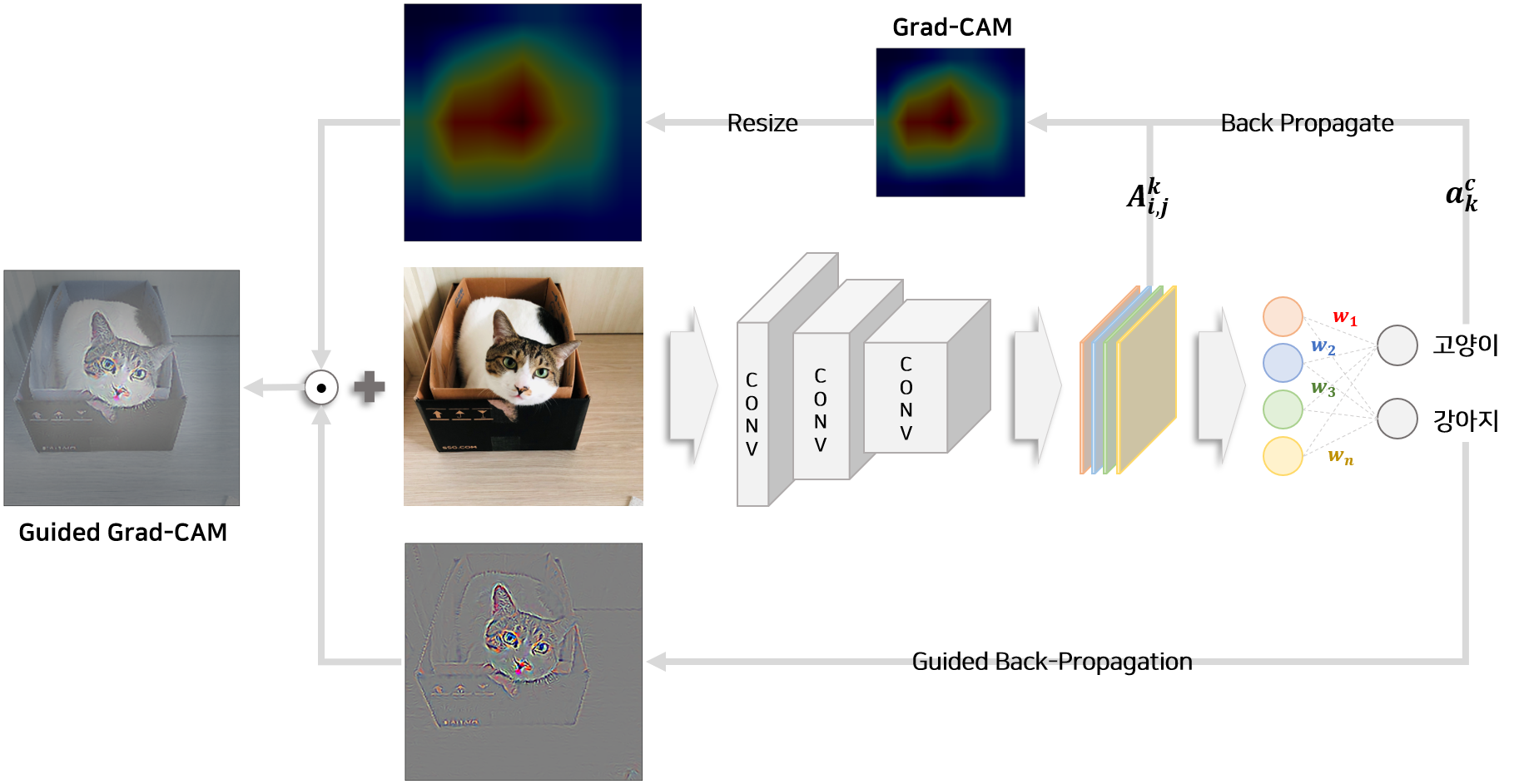
Grad-CAM은 이미지에서 클래스에 영향을 미치는 부분을 찾아낼 수 있지만 CNN layer의 feature map에 기초하여 추출되므로 CAM 이미지는 원래 이미지보다 해상도가 낮다는 단점을 갖고 있습니다. 따라서 논문에서는 class score($Y^c$)를 이용하여 원래 이미지에 gradient를 시각화 하는 다른 방법론(Guided Backpropagation, Deconvolution)들을 Grad-CAM에 함께 적용합니다. 이를 Guided Grad-CAM이라고 지칭하며 원래 이미지와 같은 해상도에서 이미지에 영향을 미치는 부분을 시각화 할 수 있습니다.

Guided Backpropagation 예시(출처)

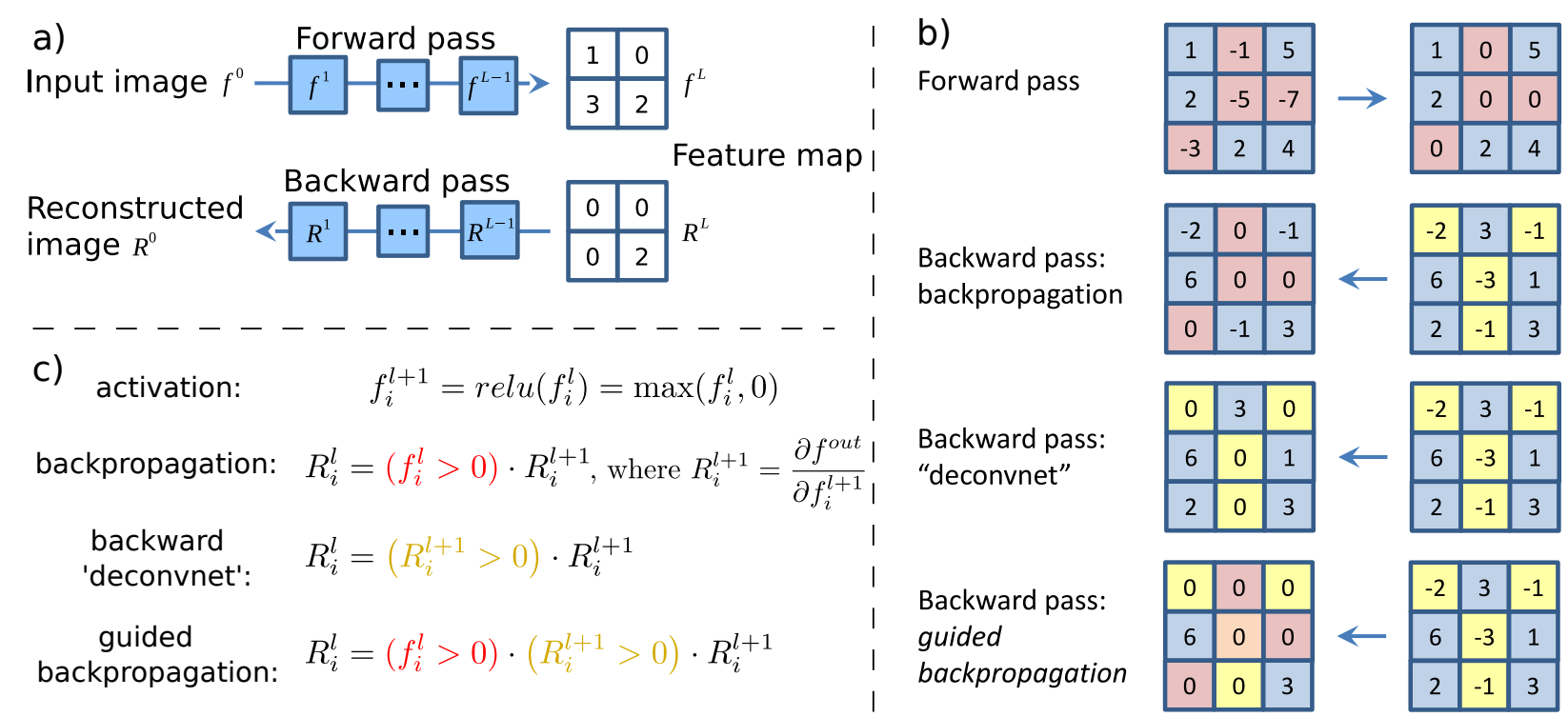
위 그림은 Striving for Simplicity: The All Convolutional Net 논문 에서 제시한 Guided Backpropagation 방법론입니다. backpropagation을 이용하여 원본 이미지로부터 highlight된 부분을 추출하는 방법에 대해 다루고 있습니다. Guided Backpropagation 핵심은 backpropation 하기전에 feature map에서 0 이하인 부분을 제거 함으로써 positive value만을 이용하여 backpropagation value를 추출합니다. 즉 음수에 해당하는 gradient를 사용하지 않음으로써 깨끗한 이미지를 추출하는 방법입니다.

Guided Backpropagation에서 추출한 image map과 Grad-CAM에서 추출한 image map은 해상도(크기)가 다르기 때문에 해상도를 맞춰야 합니다. Grad-CAM으로부터 추출된 image map의 비율을 증가시켜 원래 이미지만큼 확장합니다. 그 다음 Guided Backpropagation을 통해 생성된 image map과 element-wise 곱을 통해 Guided Grad-CAM image map을 추출할 수 있습니다.

[4] Counterfactual 추출방법

Grad-CAM을 통해 추출된 부분 이외에 네트워크의 예측에 영향을 미치는 부분을 논문에서는 Counterfactual 라고 명칭합니다.

Counterfactual 예시

논문에서 제시한 그림을 보면 이미지에 개와 고양이가 있습니다. 분류모델이 이 그림을 보고 개로 분류할 때 긍정적인 영향을 미치는 부분은 이미지에서 개가 있는 부분입니다. 반면에 모델이 이 그림을 개로 분류할 때 부정적인 영향을 미치는 부분은 고양이가 있는 부분입니다.

즉 모델이 특정 클래스로 분류할 때 방해가 되는 부분을 Counterfactual라고 합니다. Counterfactual는 Grad-CAM의 식을 변경하여 추출할 수 있습니다.

$L_{Counterfactual}^c = ReLU(-M_{i,j}^c) = ReLU(\sum_k -a_k^c A_{i,j}^k)$

결론 및 개인적인 생각

CAM 논문은 구조적 변경이 필요하기 때문에 사용하기 껄끄러운 면이 있었습니다. ResNet은 바로 적용이 가능하더라도 그 이이외에 GoogleNet, VGG 등은 CAM 논문에서 제시한 구조를 갖고 있지 않았기 때문입니다. 이러한 문제점을 모두 해결한 재미있는 논문이라고 생각합니다. CNN이 들어간 새로운 모델을 개발했을때 모델의 성능 평가 뿐만아니라 시각화를 통해 insight를 얻을 수 있을 것 같아 활용성이 높아보입니다.

뛰어난 구현체가 있으므로 바로 적용하여 시각화 할 수 있는 장점을 갖고 있습니다.

Reference

[PAPER] Grad-CAM : Visual Explanations from Deep Networks via Gradient-based Localization, ICCV 2017
[PAPER] Striving for Simplicity: The All Convolutional Net, ICLR 2015
[BLOG] Grad-CAM: 대선주자 얼굴 위치 추적기
[GITHUB] Grad-CAM implementation in Pytorch

[논문리뷰]Grad-CAM

Learning Deep Features for Discriminative Localization